While humans effortlessly discern intrinsic dynamics and adapt to new scenarios, modern AI systems often struggle. Current methods for visual grounding of dynamics either use pure neural-network-based simulators (black box), which may violate physical laws, or traditional physical simulators (white box), which rely on expert-defined equations that may not fully capture actual dynamics. We propose the Neural Material Adaptor (NeuMA), which integrates existing physical laws with learned corrections, facilitating accurate learning of actual dynamics while maintaining the generalizability and interpretability of physical priors. Additionally, we propose Particle-GS, a particle-driven 3D Gaussian Splatting variant that bridges simulation and observed images, allowing back-propagate image gradients to optimize the simulator. Comprehensive experiments on various dynamics in terms of grounded particle accuracy, dynamic rendering quality, and generalization ability demonstrate that NeuMA can accurately capture intrinsic dynamics.









Note: You can click the above radio button to apply a learned material model and change the view using the slider. We integrate NeuMA with an image-to-3D model [2] to obtain these results

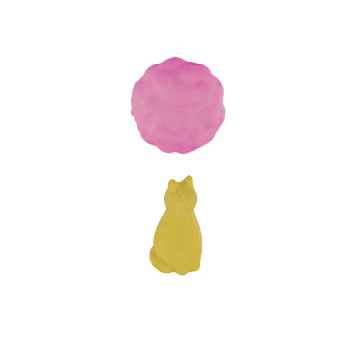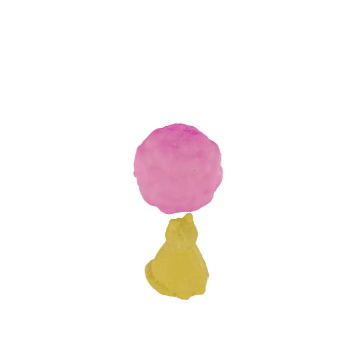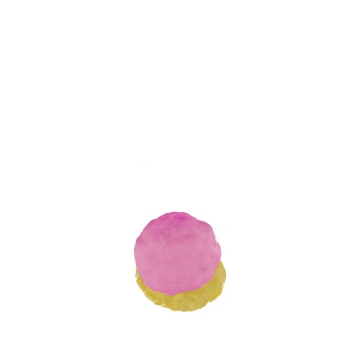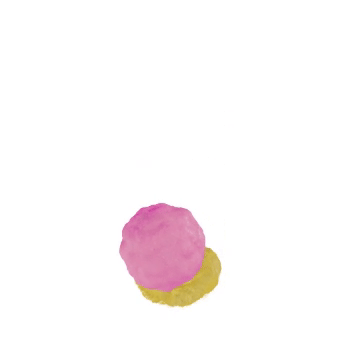



Note: The real-world data is captured by [1]
@InProceedings{Cao_2024_NeuMA,
author = {Cao, Junyi and Guan, Shanyan and Ge, Yanhao and Li, Wei and Yang, Xiaokang and Ma, Chao},
title = {Neu{MA}: Neural Material Adaptor for Visual Grounding of Intrinsic Dynamics},
booktitle = {The Thirty-eighth Annual Conference on Neural Information Processing Systems (NeurIPS)},
year = {2024}
}[1]: Zhong et al. Reconstruction and Simulation of Elastic Objects with Spring-Mass 3D Gaussians. ECCV, 2024.
[2]: Xu et al. GRM: Large Gaussian Reconstruction Model for Efficient 3D Reconstruction and Generation. ECCV, 2024.
This webpage is modified from the template provided here.